Maquinas de Estado Finito
Descripción de Hardware con Verilog
Saludos cordiales, en esta entrada, abordaremos el tema de los autómatas o maquinas de estado finito, con una breve introducción al concepto para luego realizar la descripción de este modelo utilizando en lenguaje Verilog. Es muy recomendable que el lector tenga conocimientos sobre el diseño de circuitos secuenciales, sobre todo la elaboracion de diagramas de transición.
Dejo algunos enlaces relacionados: <<Enlace 1>>, <<Enlace 2>>, <<Enlace 3>>
De aquí en adelante en la redacción utilizare los acrónimos:
- MEF(Maquina de Estado Finito)
- FSM(Finite State Machine) como referencia.
También revisaremos algunos ejemplos llevando a cabo pruebas de simulación para lo cual utilizaremos la versión altera de ModelSIM que viene instalado con el software Quartus II de Intel.
Aquí te dejo los enlaces para descarga previo registro en la pagina de intel:
<<ModelSim Standard Edition 18.1>>
Introducción al tema
 |
| Fig1. Representación conceptual de una FSM |
En términos generales, podemos definir una Maquina de Estados Finito (FSM) como un conjunto de entradas (inputs), un conjunto de estados (states) y un conjunto de salidas(outputs) cuya transición entre los estados obedecen a una función lógica, denominada función de transición. ver Figura 1.
Además, se dice “estado finito” porque la cantidad de estados es un numero determinado. Los estados son representaciones abstractas que marcan pasos en una secuencia de operaciones donde la función de transición determina el siguiente estado en cada ciclo de reloj considerando el estado actual.
Hay dos modelos conceptuales denominados Mealy y Moore, que se muestran en la Figura 2, con un diferencia muy puntual que es la siguiente:
- La salida en el modelo de Moore, depende únicamente del estado presente.
- La salida en el modelo de Mealy, depende del estado presente y la entrada.
 |
| Fig2. Representación del Modelo Mealy - Moore |
Conocida la diferencia entre ambos modelos podemos mencionar lo siguiente:
- A diferencia de Mealy, una maquina de Moore tiene la salida sincronizada con el reloj, porque depende únicamente del estado presente.
- A diferencia de Moore, una maquina Mealy usualmente utiliza menos estados para llevar a cabo la misma tarea.
Con la practica notara que estos modelos se adaptan mejor a un situación en particular. En muchos casos adoptan el modelo de Moore, porque el análisis temporal con diagramas es mas comprensible porque las salidas de la maquina cambian junto con el reloj.
Desarrollo
Llevaremos a cabo una descripción procedimental de una maquina estados considerando el modelo de Moore, para lo cual utilizare un ejemplo bastante simple.
Ejemplo #1: Maquina de estados finito (FSM) para encender y apagar una luz, utilizando solo un pulsador.
 |
| Fig3. Funcionamiento del pulsador |
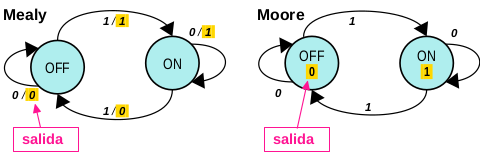 |
| Fig4. Diagrama de estados y transiciones FSM |
Note la validez del concepto descrito en la introducción, en el diagrama de Mealy la salida se establece durante la transición entre estados, reflejando una clara dependencia del estado presente con la entrada. En cambio en el modelo de Moore la salida siempre toma su valor con el estado presente.
Ahora vamos a crear un modulo descriptivo Verilog, para implementar la FSM basándonos en el diagrama de transiciones de la Figura 4, este modulo contara con una entrada(e), y una salida(s), además indirectamente se debe agregar la entrada para el reloj(clk) y también para el reinicio(rstn).
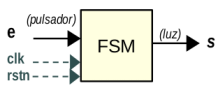 | |||||
| Fig5. Diagrama de bloque FSM | |
 |
| Fig6. Modulo descriptivo basado en el modelo Moore |
 |
| Fig7. Modulo descriptivo basado en el modelo Mealy |
Analizando el diagrama de tiempo de la Figura 7, vera que la salida se establece en el mismo tiempo donde se activa la entrada (e=1), esto porque en Mealy la salida depende tanto del estado presente como de la entrada.
Las descripciones que se observan en las Figuras 6 y Figura 7, muestran una representación bastante aproximada al concepto de ambos modelos, donde se identifica claramente las tres etapas o bloques que conforman una FSM.
Es posible simplificar la codificación, uniendo la etapa de salida (función de salida) con la entrada (función de estado siguiente) ver Figura 8, o inclusive describir las tres etapas en una misma sección como muestra la Figura 9.
 |
| Fig8. Descripción de la FSM en dos secciones |
 |
| Fig9. Descripción de la FSM en una sola sección |
 |
| Fig10. Diagrama de tiempo FSM en una sola sección |
En el modulo descriptivo final de la Figura 9 y su diagrama de tiempo (ver Figura 10), notara que el tiempo de respuesta(evento del pulsador - acción de salida) demora dos pulsos de reloj. Esto se debe a que toda la funcionalidad del circuito se describe en un solo bloque secuencial que esta sincronizada con los flancos positivos del reloj, por esta razón tanto el evento como la acción siempre se validan con el siguiente flanco de reloj.
Ahora veremos un caso mas practico y aplicable que el anterior.
Ejemplo #2: Diseñaremos una FSM para determinar el sentido de giro de un codificador rotativo, donde las entradas A (ina) y B (inb) provenientes del codificador son señales cuadradas desfasadas entre si a 90 grados, tal como se observa en la Figura 11. La salida (fwd) para indicar el sentido de giro sera uno (1) para adelante y cero (0) hacia atrás
 |
| Fig11. Operación de un codificador rotativo |
 |
| Fig12. Estados y transiciones del codificador |
La Figura 12, ilustra el diagrama de estado y transiciones para la FSM, el nombre de cada estado por ejemplo STA00, representa el momento cuando la señal en ambas entradas es A=0 y B=0. La salida (rate) permtie establecer la relación de cambio para un determinado numero de pasos(resolución), pero no se tomara en cuanta para nuestro ejemplo, y se utilizara como referencia de cambio la entrada A(ina).
Describiremos esta maquina de Mealy en las siguientes secciones:
a) Definición de los estados:
// segun entrada {AB]=00->01->11->10 Atras
localparam STA00 = 0; //Estado presente INA=0 y INB=0
localparam STA10 = 1; //Estado presente INA=1 y INB=0
localparam STA11 = 2; //Estado presente INA=1 y INB=1
localparam STA01 = 3; //Estado presente INA=0 y INB=1
reg[1:0] state, nextstate;//Registros de estado 2-bit
b) Etapa secuencial que actualiza el registro de estado presente:
always @(posedge clk, negedge rstn) //Sincronizado
if(rstn == 0) state <= STA00; //Estado inicial al reiniciar
else state <= nextstate; //Actualiza estado presente
c) Etapa combinacional que valida el estado presente, las entradas y establece el valor de salida:
case(state)
STA00: //Estado presente INA=0 y INB=0
begin
if(ina==1 && inb==0)
begin
fwd <= 1;
nextstate <= STA10;
end
else
if(ina==0 && inb==1)
begin
fwd <= 0;
nextstate <= STA01;
end
else nextstate <= STA00;
end
STA10: //Estado presente INA=1 y INB=0
begin
if(ina==1 && inb==1)
begin
fwd <= 1;
nextstate <= STA11;
end
else
if(ina==0 && inb==0)
begin
fwd <= 0;
nextstate <= STA00;
end
else nextstate <= STA10;
end
STA11: //Estado presente INA=1 y INB=1
begin
if(ina==0 && inb==1)
begin
fwd <= 1;
nextstate <= STA01;
end
else
if(ina==1 && inb==0)
begin
fwd <= 0;
nextstate <= STA10;
end
else nextstate <= STA11;
end
STA01: //Estado presente INA=0 y INB=1
begin
if(ina==0 && inb==0)
begin
fwd <= 1;
nextstate <= STA00;
end
else
if(ina==1 && inb==1)
begin
fwd <= 0;
nextstate <= STA11;
end
else nextstate <= STA01;
end
endcase
El modulo descriptivo completo se muestra en el siguiente enlace:
Para hacer la validación funcional, realizaremos un simulación de tiempos utilizando el siguiente modulo de estimulo:
module fsm_encoder_tb;
reg clk, rstn, ina, inb;
wire fwd, rate;
fsm_encoder ins0(clk, rstn, ina, inb, fwd, rate);
initial begin
clk = 0; rstn = 0; ina=0; inb=0;
forever #05 clk = !clk;
end
initial begin
#50 rstn = 1;
#50 ina=0; inb=1;
#50 ina=1; inb=1;
#50 ina=1; inb=0;
#50 ina=0; inb=0;
#100 ina=1; inb=0;
#50 ina=1; inb=1;
#50 ina=0; inb=1;
#50 ina=0; inb=0;
#20 ina=1; inb=0;
#20 ina=1; inb=1;
#20 ina=0; inb=1;
#20 ina=0; inb=0;
#20 ina=1; inb=0;
#20 ina=1; inb=1;
#20 ina=0; inb=1;
#20 ina=0; inb=0;
end
endmodule
 |
| Fig13. Diagrama de tiempos del encoder FSM |
Conclusiones
Recordar que las maquinas de estado finito conceptos fundamentales en el diseño de sistemas electronicos, y su implementación no se limita únicamente a describir el hardware de los circuitos digitales, si no que puede adoptarse en cualquier sistema informático mediante lenguajes de programación.
También mencionar que la manera de como describí la FSM con verilog no representa la única manera de hacerlo, solo me base en algunas referencias porque hay muchos libros y manuales que aplican estilos propios, pero al final utilizan el mismo principio, lo importante es hacer practicas y analizar la simulaciones para realmente comprender como se van estableciendo las condiciones y estados de la maquina. Te dejo unos enlaces de referencias para el diseño de maquinas FSM por parte de <<Intel>> y <<Xilinx>>:
Para finalizar solo quiero agradecer tu visita a mi blog, espero que el contenido de esta entrada hubiera sido de ayuda en tu formación educativa, favor cualquier consulta al respecto pueden escribirme a:
pablinzte@gmail.com / pablinza@me.com
@blinzar (Twitter)
Pablo Cesar Zárate.
